A Pitagorasz-tétel az egyik legszélesebb körben ismert matematikai tétel. A tétel a következőt mondja ki:
Ha egy háromszög derékszögű, akkor befogóinak négyzetösszege egyenlő az átfogó négyzetével.
Ezt képlettel is le tudjuk írni, ami a következőképp fest:
![]()
A Pitagorasz-tételnek létezik másik megfogalmazása is, ez pedig a következő: Ha egy háromszög derékszögű, akkor az átfogójára emelt négyzet területe megegyezik a befogóira emelt négyzetek területének összegével.

Most pedig nézzük meg, hogyan tudjuk bizonyítani a Pitagorasz-tételt.
A Pitagorasz-tétel bizonyítása
Bizonyítani akarjuk, hogy
![]()
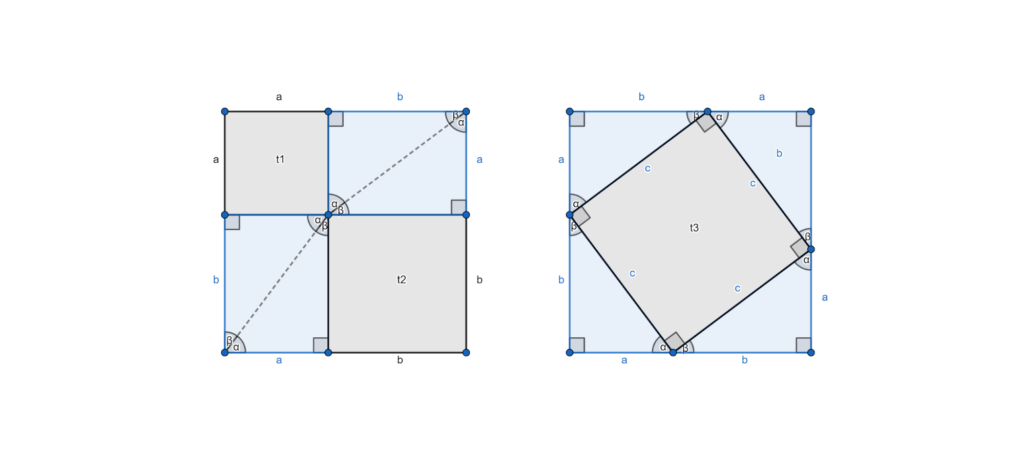
Ehhez vegyünk fel két ![]() oldalú négyzetet. A két négyzet területe egyenlő.
oldalú négyzetet. A két négyzet területe egyenlő.
Bontsuk fel az első négyzetet egy ![]() és egy
és egy ![]() területű négyzetre, továbbá 4 olyan derékszögű háromszögre, amelyek befogói:
területű négyzetre, továbbá 4 olyan derékszögű háromszögre, amelyek befogói: ![]() és
és ![]() . Ez a 4 háromszög egybevágó egymással és az eredeti háromszöggel, tehát a területük egyenlő.
. Ez a 4 háromszög egybevágó egymással és az eredeti háromszöggel, tehát a területük egyenlő.
A második ![]() oldalú négyzetben vegyünk fel egy négyszöget a következőféleképpen:
oldalú négyzetben vegyünk fel egy négyszöget a következőféleképpen:
- oldalai egyenlő hosszúak (ezek derékszögű háromszögek átfogói)
- szögei 90°-osak (egybevágó derékszögű háromszögben
 90°)
90°)
Tehát a négyszögünk egy négyzet. Vagyis ha a derékszögű háromszögek átfogója ![]() , akkor a területe
, akkor a területe ![]() .
.
Így a két nagy négyzet területéből kivonva a háromszögek területét, a fennmaradó területek egyenlőek lesznek.
Pitagorasz-tétel megfordítása
Ha egy háromszög két oldalhosszának négyzetösszege egyenlő a harmadik oldal hosszának négyzetével, akkor a háromszög derékszögű.
Pitagorasz-tétel alkalmazása
- Ha egy derékszögű háromszögben adott két oldal hossza, a tétel segítségével kiszámolható a harmadik oldal hossza.
- Ha egy háromszögben adott mindhárom oldal hossza, kiszámítható, hogy a háromszög leghosszabb oldalával szemben lévő szög milyen.
- Ha
 , akkor a háromszög tompaszögű.
, akkor a háromszög tompaszögű. - Ha
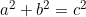 , akkor a háromszög derékszögű.
, akkor a háromszög derékszögű. - Ha
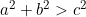 , akkor a háromszög hegyesszögű.
, akkor a háromszög hegyesszögű.
- Ha
Példa a tétel alkalmazására
Adott egy derékszögű háromszög, melynek befogói 6 cm és 8 cm. Számítsuk ki az átfogó hosszát!
A feladatból tudjuk a háromszög befogóinak hosszát:
![]()
A Pitagorasz-tétel egyenlete:
![]()
Az adatokat beírva a képletbe:
![]()
![]()
![]()
![]()
Tehát a háromszög átfogójának hossza 10 cm.
Gyakorlati példa a Pitagorasz-tétel alkalmazására
Egy vitorlás hajó árbócának a magasságát szeretnénk meghatározni. A következőket tudjuk:
- Mind a két vitorla, a fővitorla (a képen kékkel jelölve) és az orrvitorla (narancssárgával) derékszögű háromszög alakúak.
- A két vitorla átfogója megegyező hosszúságú.
- A fővitorla hajópadlóval párhuzamos oldala kétszer olyan hosszú, mint az orrvitorláé.
- A fővitorla kétszer olyan távol kezdődik a padlótól, mint az orrvitorla.
- Az orrvitorla hajópadlóval párhuzamos oldala ugyanolyan hosszú, mint amilyen magasságban a fővitorla kezdődik a padlótól számítva.
- Az orrvitorla hajópadlóval párhuzamos oldala 2 méter hosszú.

Haladjunk szépen, lépésről-lépésre. Először is írjuk fel, hogy mit kell kiszámolnunk: az árbóc hosszát, azaz az ![]() szakaszt.
szakaszt.
Jelöljük el a vitorlák oldalait, majd írjuk fel, amit tudunk. Legyen a fővitorla átfogója ![]() , befogói pedig
, befogói pedig ![]() és
és ![]() . Legyen az orrvitorla átfogója
. Legyen az orrvitorla átfogója ![]() és a befogók pedig
és a befogók pedig ![]() és
és ![]() . Ekkor adataink a következők:
. Ekkor adataink a következők:
Mivel derékszögű háromszögekről van szó, így mind a két esetben fel tudjuk írni a Pitagorasz-tételt:
![]()
![]()
Mivel tudjuk, hogy ![]() , így azt is tudjuk, hogy
, így azt is tudjuk, hogy ![]() . Ebből pedig következik:
. Ebből pedig következik:
![]()
Tudjuk, hogy ![]() és
és ![]() , azaz:
, azaz:
![]()
![]() .
.
Tudjuk továbbá, hogy ![]() és
és ![]() , azaz
, azaz ![]() .
.
Mivel ![]() , így tudjuk, hogy
, így tudjuk, hogy ![]() (mivel 2=CB+1).
(mivel 2=CB+1).
Innen pedig fel tudjuk írni azt, hogy ![]() . Helyettesítsük ezt be a
. Helyettesítsük ezt be a ![]() egyenletbe.
egyenletbe.
![]()
![]()
Azaz ![]() , tehát
, tehát ![]() .
.
Tudjuk továbbá, hogy ![]() , azaz
, azaz ![]() .
.
Tehát az árbóc hossza 7.5 méter.
