Súlyvonal fogalma
A háromszög csúcsát a szemközti oldal felezőpontjával összekötő szakasz a háromszög súlyvonala.

Tétel – A súlypont fogalma
A háromszög súlyvonalai egy pontban metszik egymást, ezt a pontot a háromszög súlypontjának nevezzük. A súlypont 1 : 2 arányban osztja fel a súlyvonalakat (az oldal felé eső szakasz : a csúcs felé eső szakasz).

Bizonyítás
Vegyük fel az ![]() háromszöget.
háromszöget.
Húzzuk be az ![]() és
és ![]() csúcsból kiinduló súlyvonalakat. Legyen ezek metszéspontja
csúcsból kiinduló súlyvonalakat. Legyen ezek metszéspontja ![]() , a szemközti oldalon lévő metszéspontok pedig
, a szemközti oldalon lévő metszéspontok pedig ![]() és
és ![]() .
.
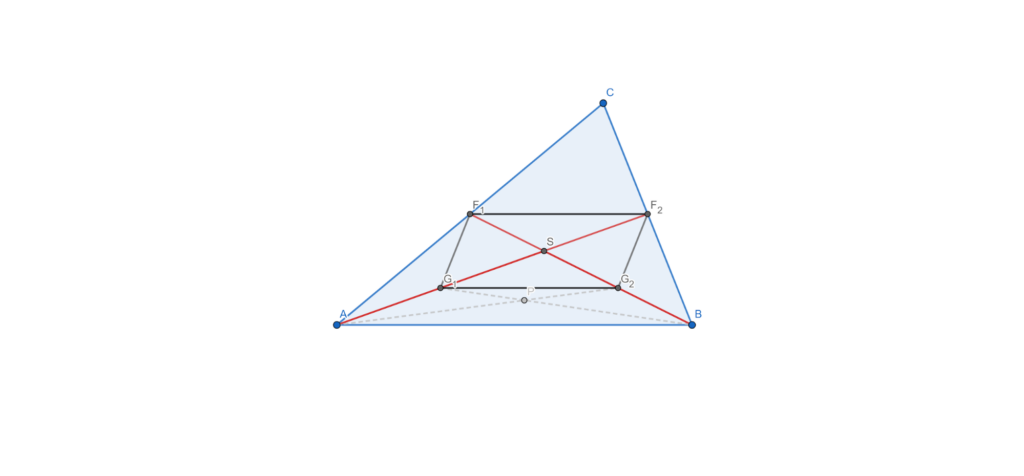
Mivel az ![]() szakasz az
szakasz az ![]() háromszög középvonala, ezért tudjuk, hogy
háromszög középvonala, ezért tudjuk, hogy
![]() ,
,
![]() .
.
Most nézzük az ![]() háromszöget. Húzzuk be az
háromszöget. Húzzuk be az ![]() és
és ![]() csúcsból kiinduló súlyvonalakat. Legyen ezek metszéspontja
csúcsból kiinduló súlyvonalakat. Legyen ezek metszéspontja ![]() , a szemközti oldalon lévő metszéspontok pedig
, a szemközti oldalon lévő metszéspontok pedig ![]() és
és ![]() .
.
Mivel az ![]() szakasz az
szakasz az ![]() háromszög középvonala, ezért tudjuk, hogy
háromszög középvonala, ezért tudjuk, hogy
![]() ,
,
![]() .
.
Ez azt jelenti, hogy
![]() ,
,
![]() .
.
Tehát az ![]() négyszög paralelogramma.
négyszög paralelogramma.
A paralelogramma egyik tulajdonsága, hogy átlói felezik egymást, vagyis
![]() ,
,
![]() .
.
\end{gathered}
\end{equation}
Mivel a ![]() szakasz az
szakasz az ![]() háromszög középvonala, ezért tudjuk, hogy
háromszög középvonala, ezért tudjuk, hogy
![]() ,
,
![]() .
.
Ez az előbbiek alapján továbbá
![]() ,
,
![]() .
.
Vagyis az ![]() aránya egyenlő lesz
aránya egyenlő lesz ![]() .
.
A bizonyítás az ![]() háromszög bármely két tetszőleges súlyvonalára igaz. Tehát a harmadik súlyvonalnak át kell haladnia az
háromszög bármely két tetszőleges súlyvonalára igaz. Tehát a harmadik súlyvonalnak át kell haladnia az ![]() ponton. Így ez a pont a háromszög súlypontja.
ponton. Így ez a pont a háromszög súlypontja.
Súlyvonal kiszámítása a háromszög oldalaiból
Vegyük fel az ![]() háromszöget és jelöljük el oldalait rendre
háromszöget és jelöljük el oldalait rendre ![]() ,
, ![]() és
és ![]() jelöléssel.
jelöléssel.
Rajzoljuk be az ![]() csúcshoz tartozó súlyvonalát. Jelöljük el ezt
csúcshoz tartozó súlyvonalát. Jelöljük el ezt ![]() -val.
-val.
Tükrözzük a háromszöget az ![]() oldalra. Ekkor egy olyan paralelogrammát kapunk, melynek oldalai
oldalra. Ekkor egy olyan paralelogrammát kapunk, melynek oldalai ![]() és
és ![]() , valamint átlói
, valamint átlói ![]() és
és ![]() .
.
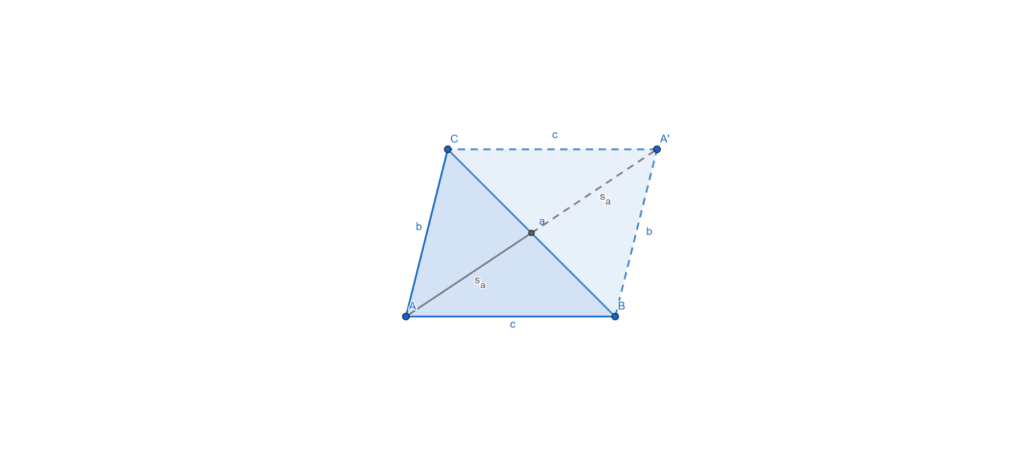
A paralelogramma egyik tulajndonsága, hogy átlóinak négyzetösszege megegyezik az oldalak négyzetösszegével. Ez esetünkben a következőt jelenti:
![]() .
.
Ebből az egyenletből az ![]() csúcshoz tartozó súlyvonal hosszát kifejezve a következőt kapjuk:
csúcshoz tartozó súlyvonal hosszát kifejezve a következőt kapjuk:
![]() ,
,
![]() .
.
A gondolatmenet a háromszög bármely csúcsára és súlyvonalára ugyanúgy alkalmazható. Így a háromszög súlyvonalainak hossza:
![]() ,
,
![]() ,
,
![]() .
.
